I recently read the paper Crystal Graph Convolutional Neural Networks for an Accurate and Interpretable Prediction of Material Properties. The authors have created an open source implementation of their technique at https://github.com/txie-93/cgcnn.
This paper proposes a new way to learn material properties directly using the structure of atoms in the crystal as input. The authors were motivated by the fact that applying traditional machine learning methods to crystalline material discovery was complicated by the fact that either manual feature transforms or complex input transformations were required. The new graph convolutional method introduced in this work allows machine learning models to directly learn from the crystal structure of the material. The method achieves similar accuracy to density functional theory (DFT) physics-based calculations for 8 properties after training on DFT data sourced from Materials Project (The https://github.com/materialsproject/pymatgen Python API for the materials project is a really cool resource worth checking out).
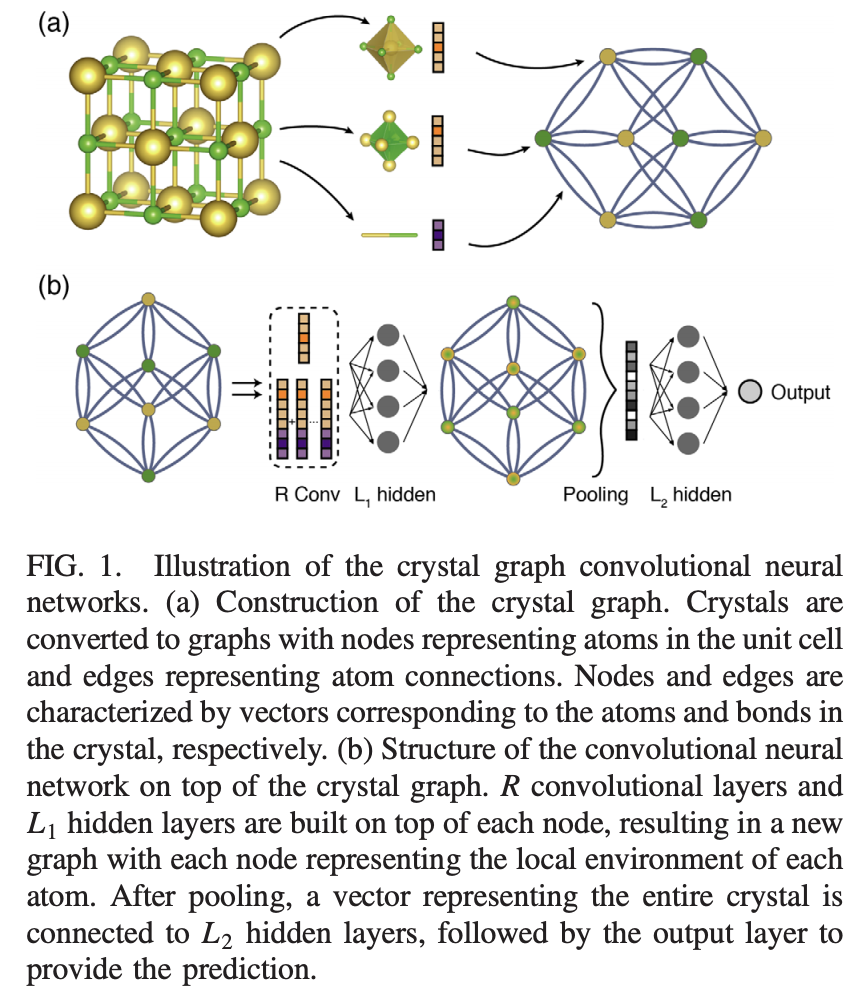
The figure above represents the basic structure of the crystal graph convolutional network. The R-convolutional layers take the crystal structure as input, passing into hidden layers, then pooling layers.
The basic mathematical idea is to treat crystal structure as a multigraph. Recall that a multigraph is a graph where nodes are permitted to have multiple edges between one another. In this multigraph, atoms are nodes and bonding interactions are edges. The multigraph aspect arises since the crystal graphs are periodic, which means that there could be “wrap-around” edges which lead to multiple connections between two nodes in the graph. For each node i, we have a feature vector v_i and for each edge (i,j)_k (representing the k-th bond between nodes i and j) we have edge feature vector u_{(i,j)_k}).
The cystal graph convolutions consist of convolutional layers and pooling layers. The basic update equation for the convolutional layers is as follows:
v_i^{(t+1)} = \textrm{Conv}\left ( v_i^{(t)}, v_j^{(t)}, u_{(i,j)_k} \right ), \ \ \ (i,j)_k \in \mathcal{G}
The convolutional layers iteratively update the atom feature vectors. Note that this update is performed multiple times, for all values of j, k for a given atom i. After R convolutional layers, the pooling layer is used to produce a joint feature vector v_c for the crystal as a whole:
v_c = \textrm{Pool} \left (v_0^{(0)},v_1^{(0)},\dotsc,v_N^{(0)}, \dotsc, v_N^{(R)}\right )
Here \textrm{Pool} is a permutationally invariant, size invariant such as \max or \textrm{Sum}. The paper uses a normalized summation operation for its pooling layer. The crystal feature vector is then passed into some number of hidden fully connected layers to effect additional transformations.
Let J(y, \hat{y}) be the cost-function. The model is trained by minimizing distance between the prediction and the DFT calculated property for that molecule from the Materials project. The authors using a training dataset of a diverse collection of inorganic crystals. The full dataset they consider has about 47,000 materials using 87 elements, 7 lattice systems, and 216 space groups (lattice systems and space groups are different ways in which the crystal’s geometry can be characterized.)
Models were trained with a 60/20/20 training/validation/test split. The authors experiment with a few different architectures. They start with a simple convolution operation:
v_{i}^{(t+1)} = g \left [ \left ( \sum_{j,k} v_j^{(t)} \oplus u_{(i,j)_k} \right ) W_c^{(t)} + v_{i}^{(t)} W_s^{(t)} + b^{(t)} \right ]
Where \oplus denotes concatenation of atom and bond feature vectors,and W_c^{(t)}, W_s^{(t)}, b^{(t)} are the convolutional weight matrix, self-weight matrix, and bias term respectively. The figure below displays with this convolution (denoted as Eq 4). This equation doesn’t perform as well as hoped. The authors suggest this may be due to the fact that W_c^{(t)} is shared across all neighbors of node i which neglects differences in interaction strength for different neighbors. The authors introduce a modified convolution operator that first concatenates neighbor vectors
z_{(i,j)_k}^{(t)} = v_i^{(t)} \oplus v_j^{(t)} \oplus u_{(i,j)_k}
And then performs convolution with the equation
v_i^{(t+1)} = v_i^{(t)} + \sum_{j,k} \sigma \left ( z_{(i,j)_k}^{(t)} W_f^{(t)} + b_f^{(t)} \right ) \odot g \left ( z_{(i,j)_k}^{(t)} W_s^{(t)} + b_s^{(t)} \right ).
Where \odot denotes element-wise multiplication and \sigma is the sigmoid function. The paper says that the addition of the multiplicative \sigma functions as a learned weight matrix that differentiates interactions between neighbors. The figure below displays results for this equation (as Eq 5).
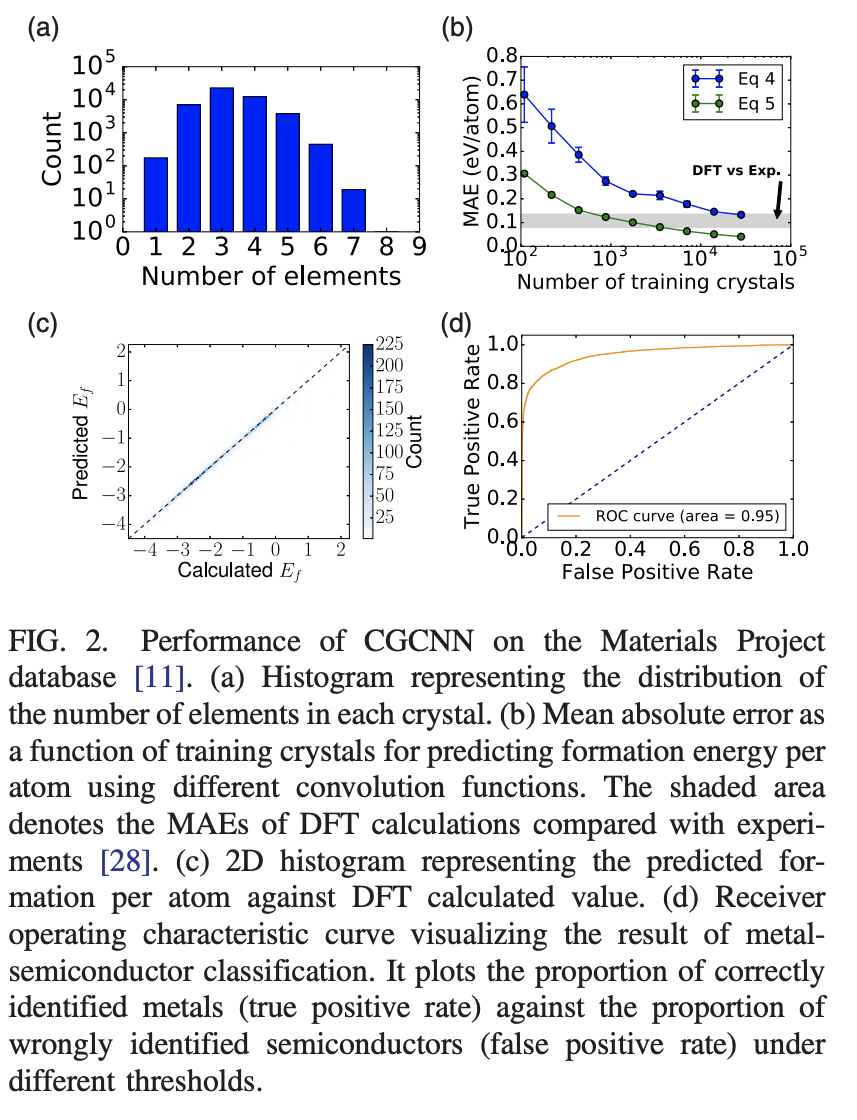
We see from the figure above that the trained models perform well in practice, capable of reaching the DFT-experimental threshold with a few thousands samples using the modified convolution operator. Figure 2(d) shows results on a binary classification task of predicting metallic/semiconductor behavior for crystals. It achieves excellent performance with a strong ROC curve.
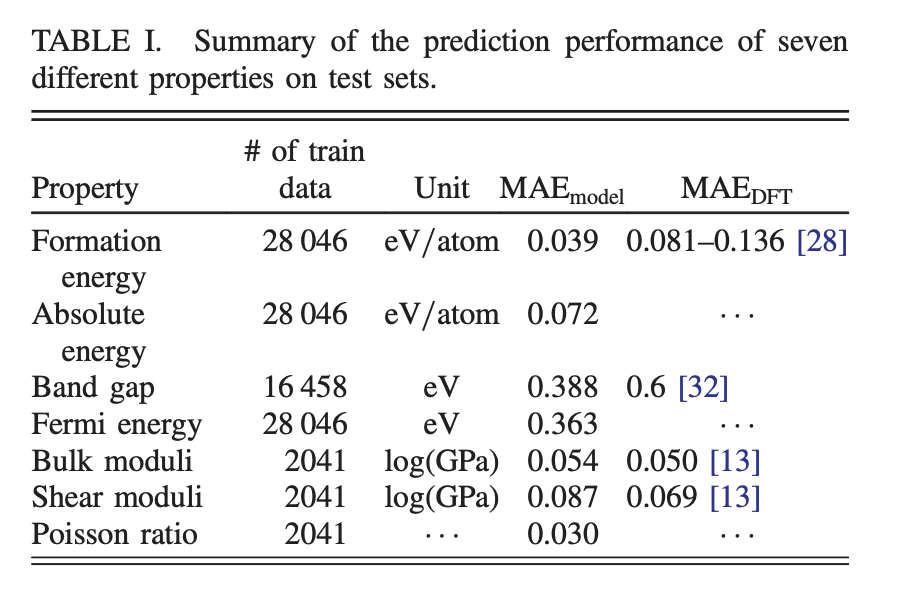
The table above demonstrates more fine-grained experimental results. The models have a reasonable amount of data to train with for each task, ranging from a few thousand to tens of thousands of datapoints.
A major design goal for the authors is to make it possible to interpret the results of the models. To do this, the authors extract the last v_i^{(R)} per-atom feature vectors, compress to a per-atom scalar \tilde{v_i}, and use these scalars to directly predict target properties via linear pooling. This linear pooling makes it possible to extract atom contributions to the model.
The paper applies this technique to the challenge of guiding the design of Perovskites. Perovskites are a type of crystal structure (see (a) in the figure below). There are three “sites”, A, B, and X in the pervoskite crystal structure. The paper applies crystal graph convolutions to the task of predicting energy above hull (the energy of decomposition into other materials that share the same composition, see the materials project glossary).
The paper uses a crystal graph convolution with linear final pooling layer to learn to predict energy above hull on a dataset of 18 thousand perovskites. This allows the authors to linearly decompose the contributions of each site to the energy above hull. Figures 3(c) and 3(d) show how different elements provide different site contributions to energy above hull.
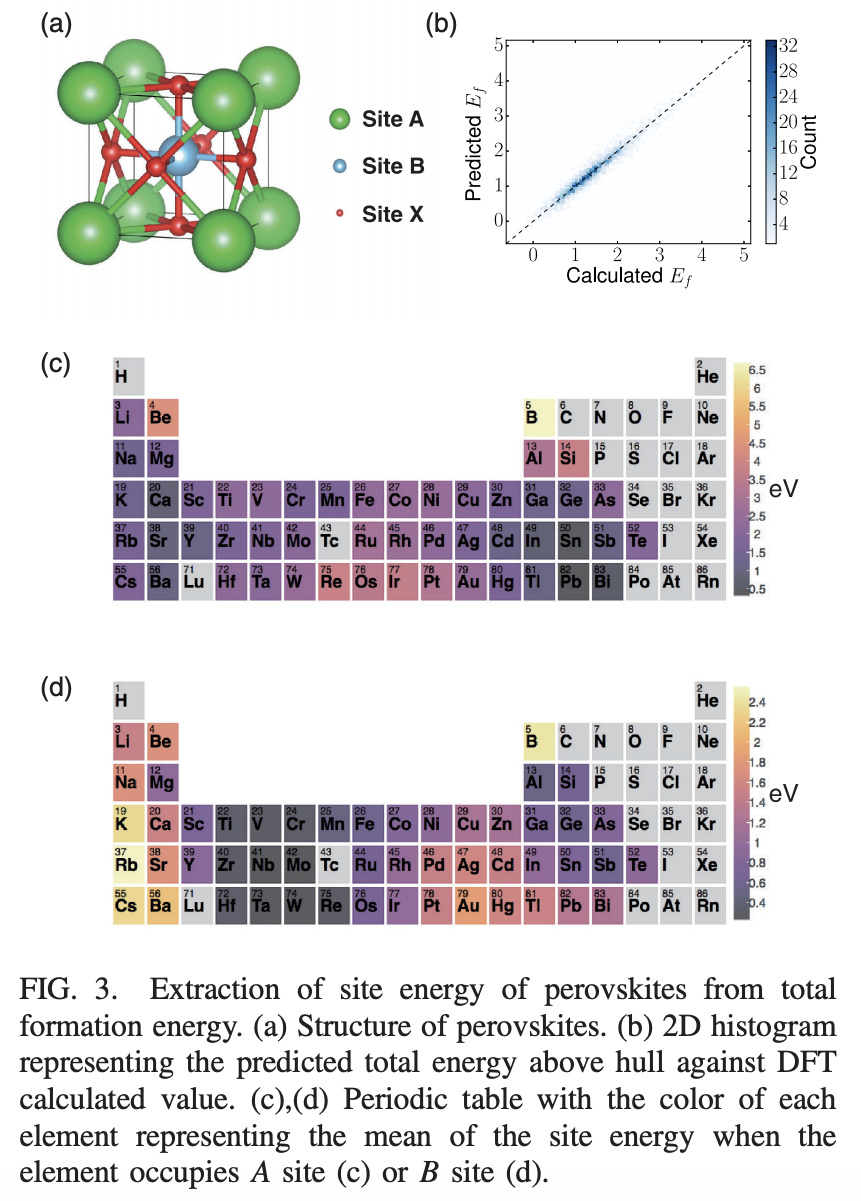
The paper uses the trained model to do a combinatorial search for stable perovskites. The model found 33 predicted stable perovskites in its search, a number of which have been experimentally synthesized elsewhere in the literature.
All in all, I found this paper really interesting. It extends the core machinery of molecular graph convolutions to an important new application area and demonstrates strong results on practical materials design task.
