The Molecular Attention Transformer is an intriguing recent work that’s come out that argues for the use of a modified transformer architecture for predicting molecular properties. There are a few key ingredients of the transformer. First, the authors augment the attention mechanism in the transformer with interatomic distances and the molecular adjacency matrix. Next, they use self-supervised pretraining to achieve improved performance. The authors have released a PyTorch implementation of their code at https://github.com/gmum/MAT.
Here’s a diagram of the Molecular Attention Transformer taken from their paper.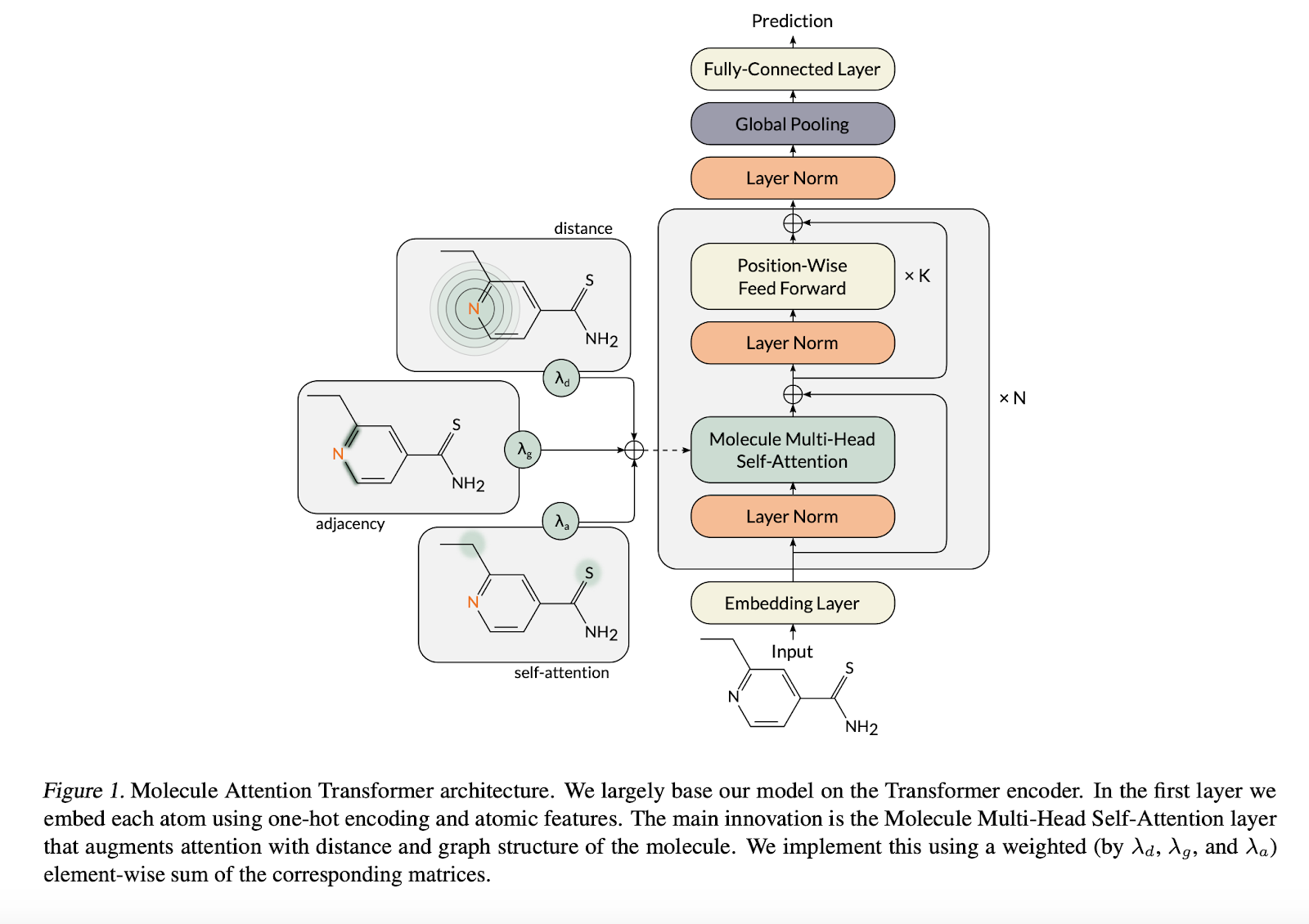
Unlike previous papers that have used transformers on molecules, here compounds are not represented as smiles strings and are represented as lists of atoms. I like this representation better than the SMILES representation since it feels like there’s less overhead for the model to learn (with SMILES, the model has to learn a working knowledge of SMILES before it can predict meaningful atomic properties).
As a brief review of the transformer architecture, a transformer consists of H heads. Head i takes in input hidden state \mathbf{H} and computes \mathbf{Q}_i = \mathbf{H}\mathbf{W}_i^Q, K_i = \mathbf{H}\mathbf{W}_i^H and \mathbf{V}_i = \mathbf{H}\mathbf{W}_i^V. This then leads to the attention operation
\mathcal{A}^{(i)} = \rho \left ( \frac{\mathbf{Q}_i\mathbf{K}_i^T}{\sqrt{d_k}} \right ) \mathbf{V}_i,
The idea behind the molecular attention transformer is to use the adjacency matrix of the molecule and the interatomic distances as additional inputs to the attention operation. This results in the equation
\mathcal{A}^{(i)} = \left ( \lambda_a \rho \left ( \frac{\mathbf{Q}_i\mathbf{K}_i^T}{\sqrt{d_k}} \right ) + \lambda_b g(\mathbf{D}) + \lambda_g \mathbf{A} \right )\mathbf{V}_i,
Here g is something like the softmax operation, \mathbf{D} the distance matrix, and \mathbf{A} the adjacency matrix. Note how this equation blends in information about the molecular structure into the attention. This version seems to require knowing the 3D pose of the molecule, but I suspect that the MAT could work reasonably well without the distance matrix (and indeed, the ablation experiments that they show later in the paper prove this out). There’s a nice elegance to this operation since it blends in molecular information naturally into the mathematical structure of the transformer.
As in graph convolutions, each atom in the molecule is encoded as a vector of chemical descriptors to start.

There are a couple of additional tricks this work uses. One of them is using a dummy node for each molecule, a type of “null atom” which roughly operates analogously to the separation token in BERT style models. The model also uses masked node pretraining. Since many datasets don’t have 3D information available experimentally, 3D conformers are computed using RDKit’s UFFOptimizeMolecule function.
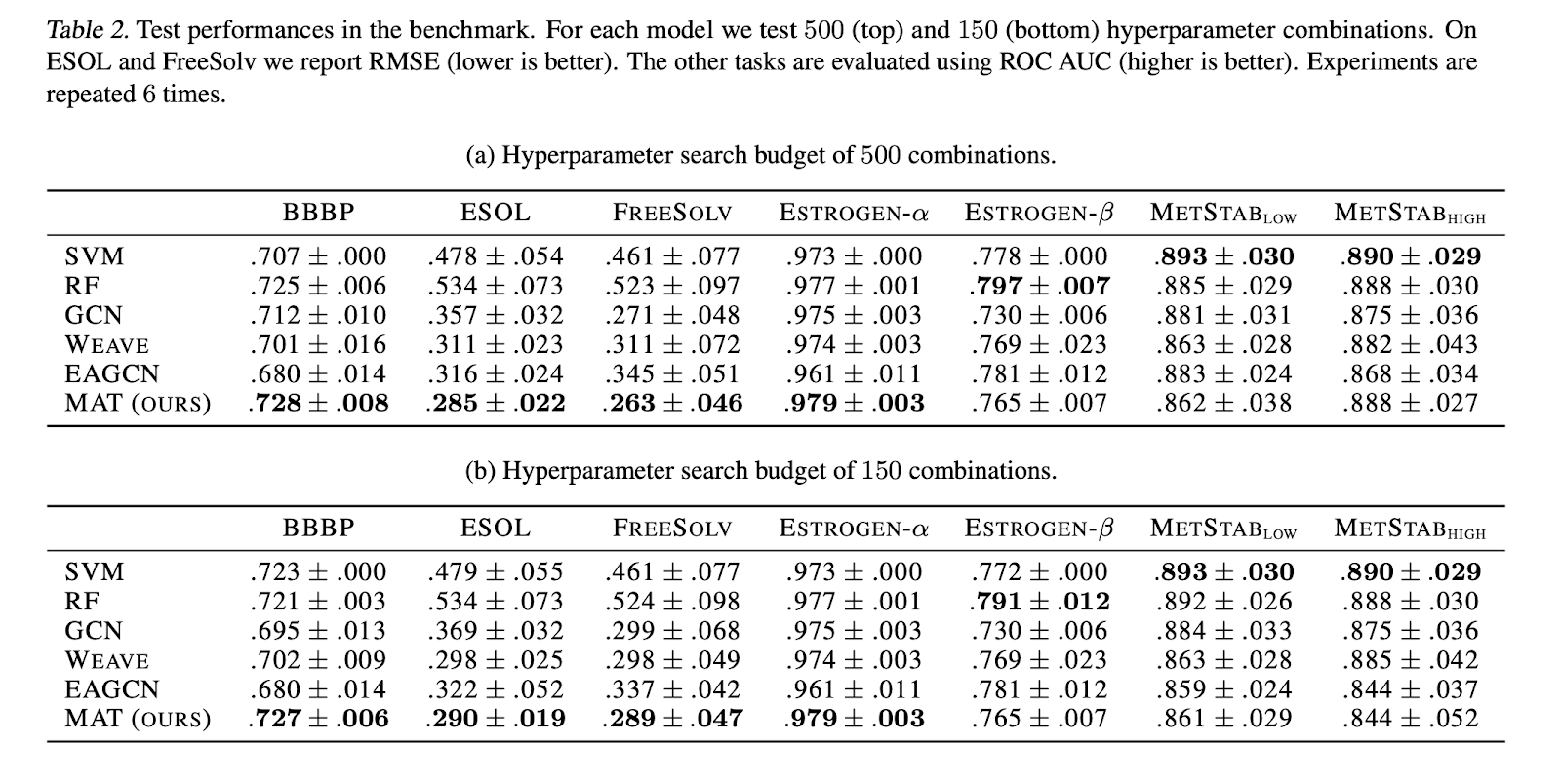
Models are tested on a number of MoleculeNet and other recent datasets. A number of baselines including random forests, edge-attention graph convolutional networks, and weave networks are used. The baseline implementations are those from DeepChem.
Models were hyperparameter tuned using either 150 or 500 different random choices of hyperparameters for tuning.
The paper does a few ablation studies where they test how the presence of the dummy node, the distance matrix, and the use of additional edge features impact the model.
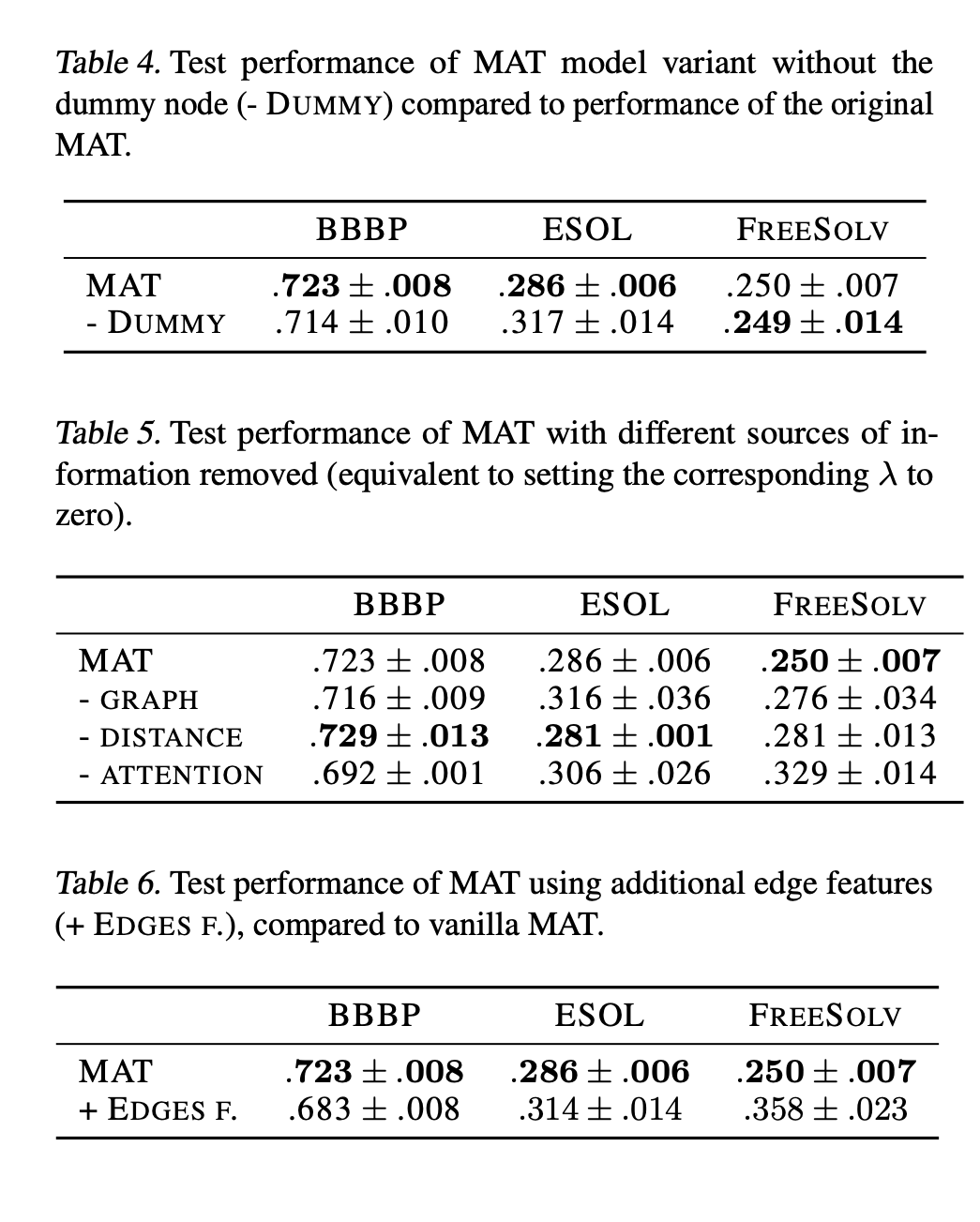
The dummy node seems to add some performance improvements, but the distance measure seems to be of middling value. This intuitively makes sense to me since the RDKit conformers are generated without any knowledge of the underlying physical system and we’re using only one conformer for modeling.
Looking at the attention layers of the molecular transformer seems to yield some insight into what the molecule is focusing on as well.
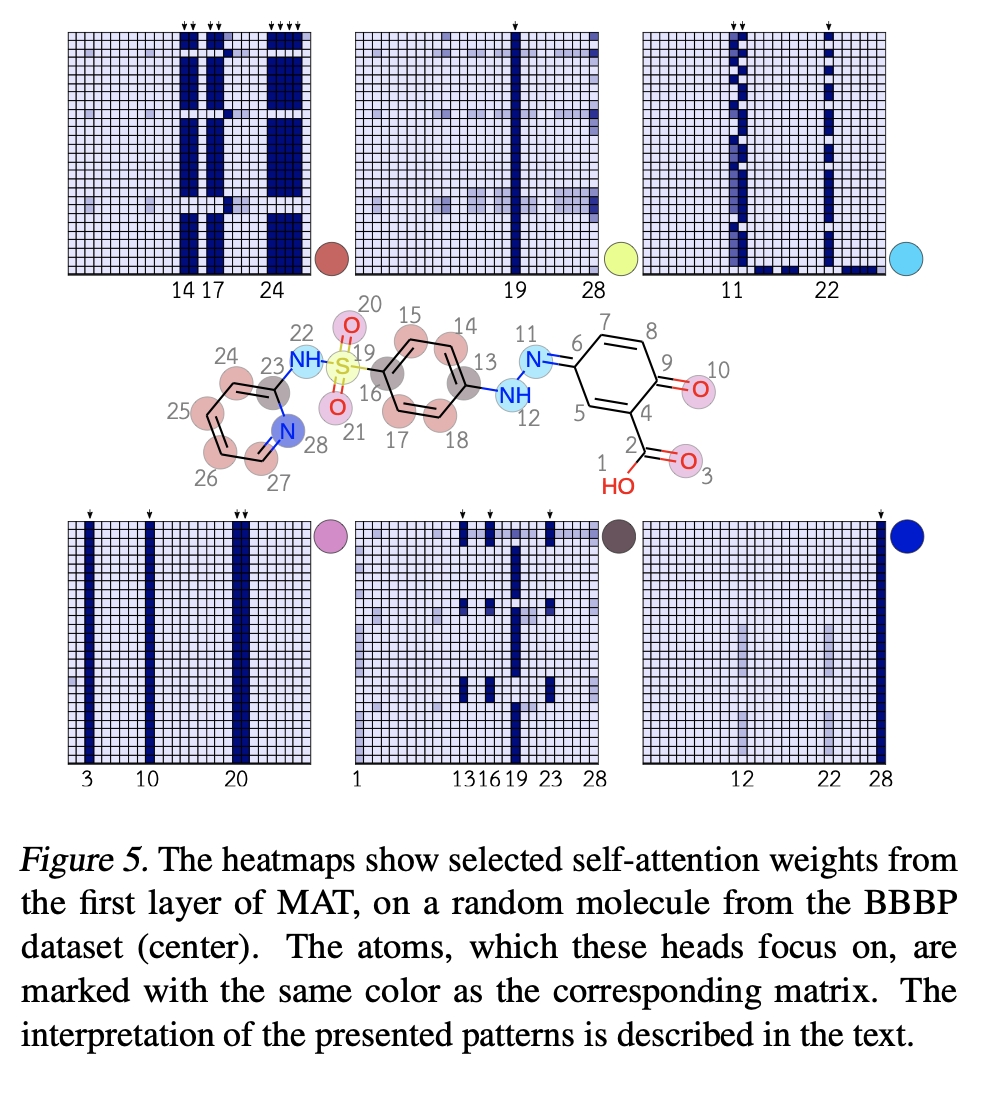
As an overall summary, the molecular attention transformer is a nice addition to the literature. It has strong performance that beats out a number of the standard DeepChem models on a collection of benchmarks. I think it would be worth adding an implementation to the DeepChem codebase.

