
This summer, I contributed to Google Summer of Code 2025 with DeepChem, working on implementing the Fourier Neural Operator, a powerful architecture for learning the solution operators of PDEs.
In this forum post, I’ll provide a detailed summary of the tasks I worked on and the progress I made over the summer.
Project Title: Fourier Neural Operator (FNO)
My project focused on implementing the FNO and integrating and wrapping it with DeepChem’s native classes.
Relevant Profile Links
Project page: https://summerofcode.withgoogle.com/programs/2025/projects/pCUg5nMr
My Github: https://github.com/spellsharp
My LinkedIn: https://www.linkedin.com/in/shrisharanyan/
Deepchem: https://deepchem.io/
Deepchem GitHub: https://github.com/deepchem/deepchem
Weekly Slides Deck: Slides
Preface
Fourier Neural Operators (FNOs) are a type of machine learning model designed to learn mappings between functions, like turning an initial condition of a physical system into its future state, by working directly in the frequency (Fourier) domain rather than on raw grid points[1]. This makes them fast, scalable, and well-suited for scientific problems where the governing rules are expressed as partial differential equations (PDEs). For DeepChem or scientific ML, FNOs matter because they can approximate the dynamics of complex systems (like fluid flow, quantum interactions, or reaction kinetics) orders of magnitude faster than traditional solvers while retaining good accuracy[1,2].
Table of Contents
- Pull Requests
- FNO vs Traditional Architectures
- Architecture & Mathematical Insight
- Usage Example
- Visual Results
- Acknowledgments
- References
Pull Requests
- #4421 – SpectralConv layer + tests (Merged)
- #4466 – FNOBlock layer + docs + tests (Merged)
- #4482 – Patch for SpectralConv layer (Merged)
- #4491 – FNO class extending Torch’s nn.Module class (Merged)
- #4492 – FNOModel: TorchModel wrapper around FNO nn.Module class (Merged)
- #4526 – Tutorial for FNOModel (Pending)
FNO vs Traditional Architectures
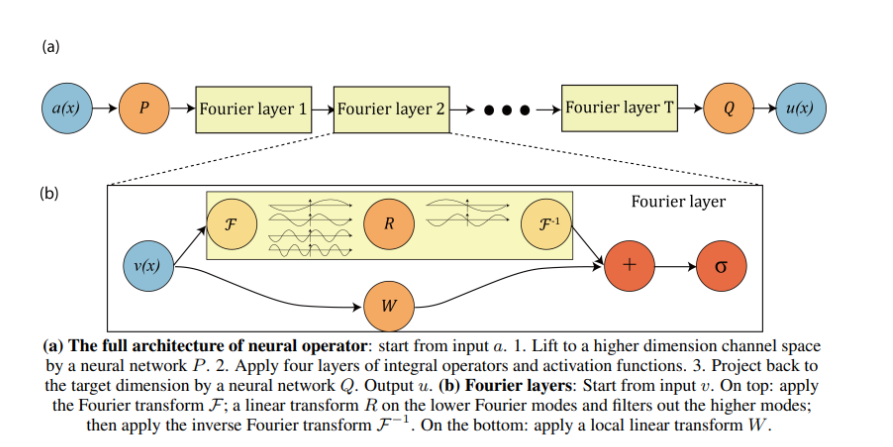
Image taken from official FNO paper
Traditional neural networks, like CNNs and RNNs, are designed to work with fixed-size inputs such as images or sequences, which are essentially fixed-length arrays of numbers. Because of this, they struggle when trying to learn solutions to partial differential equations (PDEs), which involve functions defined over continuous spaces (like time or space) and can vary in resolution or size. Neural Operators are a new kind of neural network designed to handle this challenge[3]. Instead of learning mappings between fixed-length vectors, they learn mappings between entire functions, making them much better suited for solving PDEs, even when the input data comes in different sizes or resolutions.
The FNO takes this idea further by using the Fourier transform, a mathematical tool that allows the model to understand patterns in the input on a global scale[1]. This helps the model capture long-range interactions and spatial dependencies more effectively. FNO is particularly powerful for solving PDEs because, in many real-world situations, the important behavior of a solution can be described using just a few key patterns or frequencies. By focusing on those and ignoring the noisy, less important details, FNO learns faster and generalises better[4].
Architecture & Mathematical Insight
The key idea behind FNOs is to project input data into the Fourier domain, apply learnable transformations to a selected number of Fourier modes, and then transform the result back to the spatial domain[1]. This enables the model to learn global operators with fewer parameters and improved generalization compared to standard convolutional neural networks.
Given an input function ( u(x) ), the FNO layer operates as follows:
-
Fourier Transform:
Compute the Fourier transform of the input function u(x):
\hat{u}(k) = \mathcal{F}[u](k) = \int u(x) \exp(-2\pi i k x) dx -
Spectral Convolution:
In the Fourier domain, apply a learnable linear transformation to the first m modes:
For |k| < m: \hat{v}(k) = W(k) \cdot \hat{u}(k)
For |k| \geq m: \hat{v}(k) = 0
(Here, W(k) are learnable weights for each mode.) -
Inverse Fourier Transform:
Transform back to the spatial domain:
v(x) = \mathcal{F}^{-1}[\hat{v}](x) = \sum_k \hat{v}(k) \exp(2\pi i k x) -
Nonlinearity and Stacking: The output is typically combined with a local (pointwise) neural network and passed through a nonlinearity, and multiple such layers are stacked to form the full FNO.
Results and Visualization
I trained the FNOModel for 20 epochs on a synthetic 1D Heat Equation dataset with 1,800 samples. The heat equation models how heat diffuses across a surface over time. As shown in the image, the model captured the dynamics fairly well, achieving a mean absolute error of ~0.004996 on a 200-sample test set. With additional training epochs and a more robust dataset, the model’s performance is expected to improve further.
Usage Example
# Imports
import torch
import deepchem as dc
from deepchem.models.torch_models import FNOModel
# Example data
x = torch.randn(1, 16, 16, 1)
dataset = dc.data.NumpyDataset(X=x, y=x)
# Define model architecture
model = FNOModel(in_channels=1, out_channels=1, modes=8, width=32, dims=2)
# Training the FNOModel
loss = model.fit(dataset)
# Running inference on the trained model
predictions = model.predict(dataset)
Acknowledgement
I am deeply grateful to my mentor Dr. Bharath Ramsundar for his guidance and support throughout the summer. Special thanks to José A. Sigüenza and Rakshit Singh for their mentoring and support.
Contributing to this organization has been an invaluable experience. This journey has sharpened my ability to think critically about complex problems while working alongside a community of passionate scientists and engineers. It has also given me practical skills and confidence that I’ll carry forward into research and industry alike. I’m deeply grateful to DeepChem for the opportunity.
References
-
Li, Z., Kovachki, N., Azizzadenesheli, K., Liu, B., Bhattacharya, K., Stuart, A., & Anandkumar, A. (2021). Fourier Neural Operator for Parametric Partial Differential Equations. International Conference on Learning Representations (ICLR). arXiv:2010.08895
-
Li, Zongyi. (2020, December 2). Fourier Neural Operator Blog. Provides an accessible introduction to FNO fundamentals, including mesh-invariance and speed advantages.
-
Kovachki, N., Li, Z., Liu, B., Azizzadenesheli, K., Bhattacharya, K., Stuart, A., & Anandkumar, A. (2022). Neural Operator: Learning Maps Between Function Spaces With Applications to PDEs. Journal of Machine Learning Research, 24, 1–97.
-
Qin, S., Lyu, F., Peng, W., Geng, D., Wang, J., Gao, N., Liu, X., & Wang, L. (2024). Toward a Better Understanding of Fourier Neural Operators: Analysis and Improvement from a Spectral Perspective. arXiv:2404.07200v1.
-
NeuralOperator (2021–2025). NeuralOperator: Official Implementation of Fourier Neural Operator and Related Models. GitHub repository

