Preface
For the past 4 months, I’ve worked with Deepchem via Open Chemistry as a contributor to Google Summer of Code ‘22. The scope of Deepchem aims to democratize the application of deep learning in materials science, quantum chemistry, drug discovery, and biology. Deepchem’s repo is available on GitHub where several deep learning models, layers, and examples are helpful for cheminformatics and bioinformatics developers.
TensorFlow, Keras, and PyTorch are the most prominent libraries used for building DL and ML models. The use of PyTorch, as the primary backend for building algorithms, is growing due to its sustainability. Lately, DeepChem has decided to port some TensorFlow models to PyTorch. This project aims to migrate the Normalizing Flow model with its layers and a tutorial.
We will be exploring the path and work that I’ve developed this summer.
The title of my project was The Porting of Normalizing Flow model from TensorFlow to PyTorch. In general, Normalizing Flow is a generative model which performs non-linear transformations between two probability distributions. Following DeepChem’s scope, this model aims to generate molecules and contribute to drug discovery. For the completion of this project, the list of deliverables was organized as:
- Application Affine transformation.
- Implementation of Normalizing Flow model.
- Implementation of Real NVP transformation.
- Completion of a tutorial on Training a Pytorch Normalizing Flows on Molecular Data.
All of the code include unit tests, doctests, and documentation. The presented blog is structured as follows:
- Generative models in Drug Discovery - Introduction
- Normalizing Flows and Layers
- Implementation with Pytorch
- Application of Model - Tutorial
- Acknowledgment
Generative models in Drug Discovery - Introduction
The importance of drug discovery lies in identifying new molecules that will have an impact in fields such as treating diseases, contributing to material science, climate changes, etc. Nowadays, molecules are studied, designed pathways, synthesized, and test them. Naturally, this is time and cost-consuming. The price of reactants, solvents, catalyzers, and equipment can highly depend on the reaction nature and raw material disponibility. Also, there are reactions and experiments that take time to be produced and time that is invested in pre and post-treatment in the process. A generative model is being an interesting field of study not only in terms of time and cost, and crucial resources but also in terms of feasibility. Recent studies have shown that there are around 10e8 molecules humans have synthesized, but theoretically, there are between 10e23 and 10e60 molecules in nature.
An important understanding of these models is that generative deep learning models yield a molecule without knowing the octet rule or bondings. The outputs are based on some initial features such as properties or structure of the input data. Furthermore, generative models need further research for the generative models to have a strong impact on drug discovery. Nevertheless, generative models show remarkable results in terms of cost, time, and practicability, and an implementation in Python was merged in Deepchem’s repo.
Normalizing Flows and Layers.
Studies had shown that the main deep learning architectures used for generative models in drug discovery are: variational autoencoder (VAE), generative adversarial networks (GAN), and normalizing flows. As a comparison, VAE and Normalizing Flow aim to maximize the likelihood of the data while GAN discriminates the real and fake data. Normalizing flow models gives advantages over variational autoencoders (VAE) and generative algorithms because of ease in sampling by applying invertible transformations (Frey, Gadepally, & Ramsundar, 2022).
Molecules generated through a Normalizing Flow algorithm are high dimensional data (between 3000-4000 columns) that are sampled from a base distribution (e. G., Normal distribution) and applied a concatenation of several invertible transformations (flows). Representation of Normalizing Flows workflow is presented in Fig 1. In this figure, the training data is noted as z0 while the invertible transformations are fi(zi-1). As it is shown, after applying the transformations, the user can sample from the learned distribution (zk), where it is a probability distinct from 0 to get a new molecule.
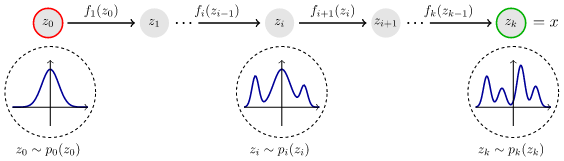
Fig 1. Normalizing Flow Workflow
In terms of the Normalizing Flow model, there are two main methods to perform: obtain a sample and calculate the logarithm of probability. To obtain a sample, the model needs an input (train data) to perform the invertible transformations, and the logarithm of probability computes the probability to get that input in the learned/transformed distribution. The transformations that will cause the changes in the base distribution are the layers. A crucial characteristic of the layer is that they must be invertible, this is differentiable and has an inverse. This is because, when working with high-dimensional data, a matrix is formed and this must have an invertible property. The following equation of Normalizing Flows will clear this idea.
log(px(x)) = log(pz(f-1(x))) + ∑ log |det(𝝏f-1(x)) / 𝝏(xi) |
In this equation, the transformation is f-1(x) and when working with high dimensional data the second term of the right becomes the sum of the logarithm of the Jacobian determinant. Notice, that this term will cause the distribution to learn according to the jacobian (rate of change).
Implementation with Pytorch.
Now, let’s take a look at the code of Normalizing Flow and the layer using Pytorch. The Pull Request for the implementation follows:
For a weekly detailed description of this project, please visit the forum post.
First, the Affine transformation/layer must perform the forward and inverse pass of the model. The code that is associated with the layer is presented:
Class initialization:
super()._init_()
self.dim = dim
self.scale = nn.Parameter(torch.zeros(self.dim))
self.shift = nn.Parameter(torch.zeros(self.dim))
The forward method:
y = torch.exp(self.scale) * x + self.shift
det_jacobian = torch.exp(self.scale.sum())
log_det_jacobian = torch.ones(y.shape[0]) * torch.log(det_jacobian)
return y, log_det_jacobian
The inverse method:
x = (y - self.shift) / torch.exp(self.scale)
det_jacobian = 1 / torch.exp(self.scale.sum())
inverse_log_det_jacobian = torch.ones(x.shape[0]) * torch.log(det_jacobian)
return x, inverse_log_det_jacobian`
For this implementation, the associated equation for the transformation looked as:
y = exp(a) * x + b
Where the learnable parameters are “a” and “b”.
Then, the Normalizing Flow model was developed. The main methods are “log_probability” and “sample” as discussed in the previous section. A general example of the code is provided:
Initialization:
self.dim = dim self.transforms = nn.ModuleList(transform) self.base_distribution = base_distribution
Log probability method:
log_prob = torch.zeros(inputs.shape[0]) for biject in reversed(self.transforms): ... inputs, inverse_log_det_jacobian = biject.inverse(inputs) log_prob += inverse_log_det_jacobian return log_prob
Sampling method:
outputs = self.base_distribution.sample((n_samples,)) log_prob = self.base_distribution.log_prob(outputs) for biject in self.transforms: outputs, log_det_jacobian = biject.forward(outputs) log_prob += log_det_jacobian return outputs, log_prob
Finally, the implementation of the Real NVP layer is used as an alternative for Affine transformation.
The real NVP layer is a normalization of Masked Affine transformations. This means that a mask is built inside the layer with a latent space, previously specified by the user. The Real NVP layer has shown better results than Affine transformation because of ease in computation. The base code, without the documentation, is presented:
Initialization:
self.mask = nn.Parameter(mask, requires_grad=False) self.dim = len(mask) self.s_func = nn.Seuential( nn.Linear(in_features=self.dim, out_features=hidden_size), nn.LeakyReLU(), nn.Linear(in_features=hidden_size, out_features=hidden_size), nn.LeakyReLU(), nn.Linear(in_features=hidden_size, out_features=self.dim)) self.scale = nn.Parameter(torch.Tensor(self.dim)) self.t_func = nn.Sequential( nn.Linear(in_features=self.dim, out_features=hidden_size), nn.LeakyReLU(), nn.Linear(in_features=hidden_size, out_features=hidden_size), nn.LeakyReLU(), nn.Linear(in_features=hidden_size, out_features=self.dim))
Forward method:
x_mask = x * self.mask s = self.s_func(x_mask) * self.scale t = self.t_func(x_mask) y = x_mask + (1 - self.mask) * (x * torch.exp(s) + t) log_det_jacobian = ((1 - self.mask) * s).sum(-1) return y, log_det_jacobian
Inverse method:
y_mask = y * self.mask s = self.s_func(y_mask) * self.scale t = self.t_func(y_mask) x = y_mask + (1 - self.mask) * (y - t) * torch.exp(-s) inverse_log_det_jacobian = ((1 - self.mask) * -s).sum(-1) return x, inverse_log_det_jacobian
Application of Model - Tutorial.
There is an existing Normalizing Flow model and tutorial made by N. C. Frey using Tensorflow as the backend. According to this, tutorial and research in FastFlows conducted in collaboration with Bharath Ramsdundar, the author proposes to generate molecules by learning the features through the Tensorflow Normalizing Flow. In this work, the QM9 dataset was used as molecular data. These SELFIES format molecules were treated and transformed into one hot encoding. Once the data was numeric binary (0 and 1), a random component was added to each entry. This part was included to make a more smooth distribution of data. Then, the model was initialized and the layer was defined using the TensorFlow probability package. With the vectors prepared and split in train and test, the model got to run with .fit command. Then, a sampling of 10 molecules was performed. Since the data is smooth, this is float, a function was called to follow a binary behavior. Finally, with the samples in one hot, they were transformed back to selfies and displayed using RDKit. Here some of the molecules are presented.
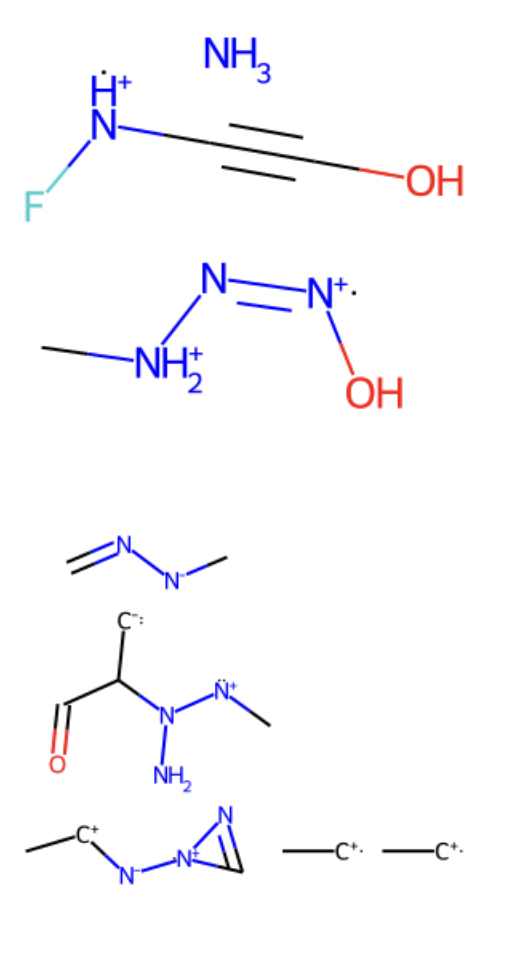
It is important to notice the ionic character of the generated samples.
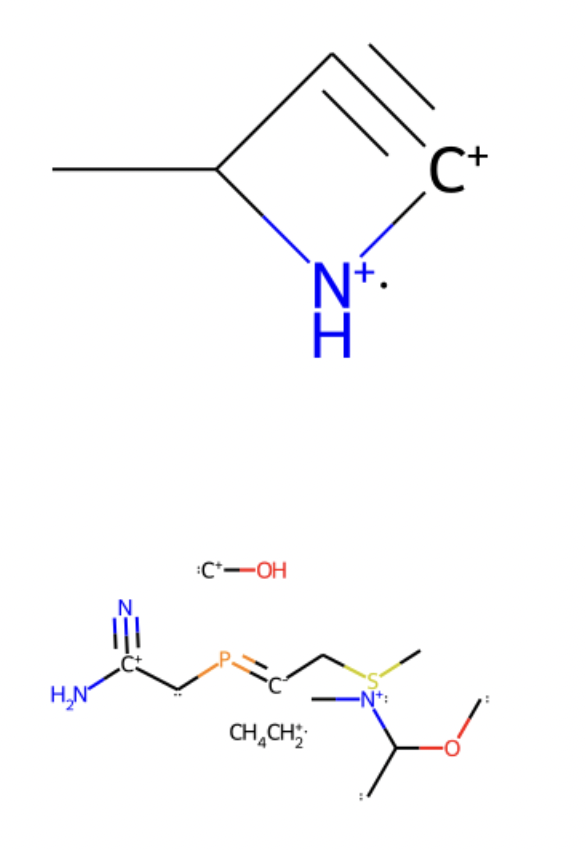
The Pytorch tutorial implementation was very similar to the TensorFlow and for instance, some problems of stability were constantly involved. Then, by applying different transformations, the results were reproduced. 10 molecules were generated and successfully displayed:
Acknowledgment
A Normalizing Flow and its layer were developed using Pytorch as the backend. I’ve seen stability problems and my suspicion is because of the layer. Some new layers must be constructed for the model to perform as expected. In terms of the tutorial, it was trained following Pytorch’s API. In order for this tutorial to get merged in DeepChem’s repo, it must follow the organization API and some work must be done. I’m still working on it, and as soon it is fixed this part will be edited. This was an amazing experience and it was possible because of the help of mentors and mentees, especially Dr. Ramnsundar from whom I have always felt guided and supported.
