Ferminet Model for deepchem
I had the opportunity of being a Google Summer of Code contributor with DeepChem (Open Chemistry), an open-source organization aiming to provide deep learning tools for drug-discovery, material science, quantum chemistry, etc.
Overview & Background Information:
In this post I aim to summarize the work that I have carried for the past 5 months (Jun-Oct).
The aim of my project was to add the the model Ferminet, which aims to predict Ab-initio(without any external data) solutions of multi-electron wave functions as accurately as possible using fewer computations. The quantum mechanical solution of molecular systems can give the ground state energy and other physical properties of a molecule like ionization, electron affinity all from computer simulation, which can save time and effort!! .
The electrons in a molecule are quantum mechanical in nature, meaning they do not follow classical physical laws. Quantum mechanics only gives a probability of where the electrons will be found and will not tell exactly where it can be found. This probability is given by the squared magnitude of a property of molecule system called the wave function and is different in each case of different molecule.These calculations are done by calculating a quantum mechanical property of the molecule system called the wave-function
For many purposes, the nuclei of the atoms in a molecule can be considered to be stationary, and then we solve to get the wave-function of the electrons. The probabilities, when modeled into 3 dimensional space, take the shape of the orbitals. Like shown in these images below which is taken via electron microscope.
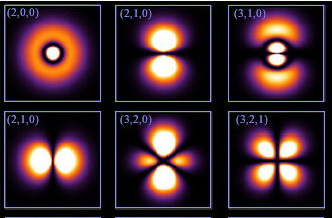
(source: Google Images)
From the top left, orbitals in order - 2s, 2p(y),3p(y),2p(x),3d(z^2),3d(x^2-y^2))
(Don’t worry if you cannot remember or relate to the concept of orbitals, just remember that these are the space where electrons are found with more probability. If you want to dig deep, I would recommend checking this great resource out. )
Presently there are many methods for the wave-function calculation, each method has its own tradeoff between the accuracy of the solution and the time complexity. Typically, the complexity of all the algorithms depend on the total number of electrons and nuclei as there will be more electron-electron and electron-nucleus interaction to be taken in account for. One such method is the Hartree-Fock, which is a very popular algorithm for approximating the wave-function in less time by ignoring the electron-electron interactions. There is also a class of algorithms which operate on the solutions of Hartree-Fock as the baseline and incorporate the missing electron-electron interactions to make it more accurate.
Ferminet uses DNNs to approximate one-such “post Hartree-Fock ‘’ method called the Variational Monte Carlo. In short, Variational Monte Carlo(VMC) samples electrons from Markov-Chain Monte Carlo(MCMC) initially via a normal distribution around the nuclei and then calculates the wavefunction, which is then again fed into the MCMC sampler to sample electrons improving the electrons’ coordinates in each iteration of the loop, aiming to minimize the ground state energy of the system(least possible energy system will be the most stable ground state molecule). In ferminet we use this same procedure, but use DNNs to approximate the wavefunction whose weights are changed from using the energy of the system as loss in each iteration of training. All this from using only the coordinates of the nuclei of the molecules as the only input.
Thus I have divided my project into the following sub-parts, implementing them one by one:-
-
MCMC sampler
-
KFAC-optimizer
-
Ferminet Model
-
1. MCMC sampler:
Markov-chain Monte Carlo is a method primarily used for taking samples from a probability distribution function. The image shown below explains it further well:
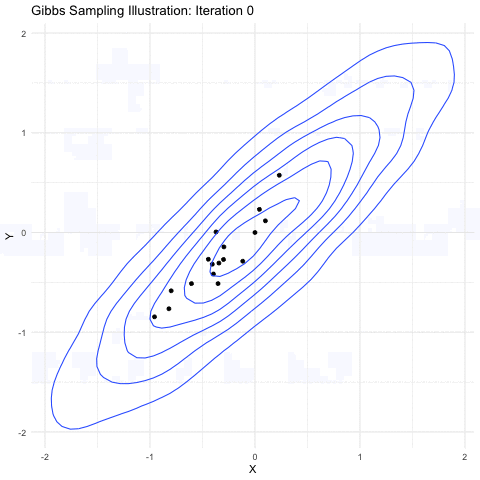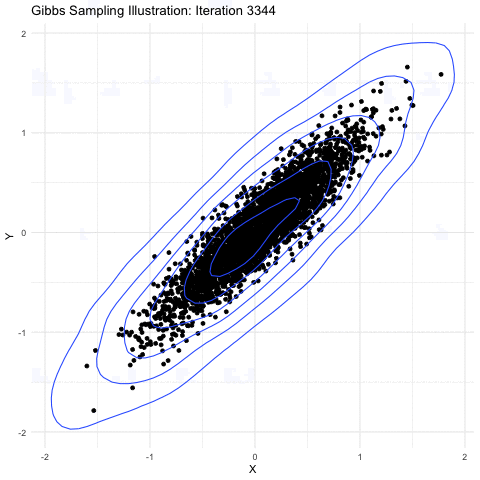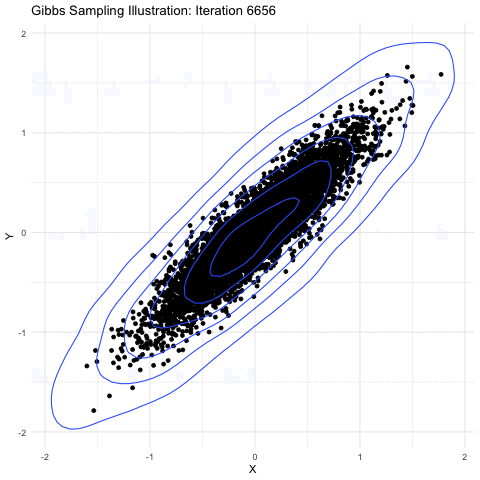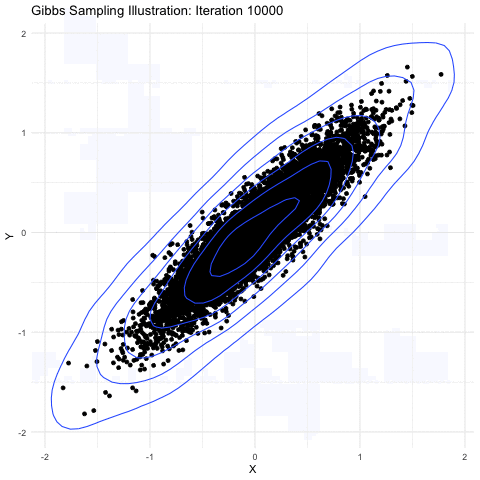
(source: Google Images)
Here, we are sampling from a 3-D gaussian distribution and as you can see here,the more samples you take, the closer it is to the normal distribution(a lot of points get accumulated in the center). This property is particularly useful as the square of the magnitude of wavefunction gives the probability of the electron in 3-D space. Hence, a MCMC sampler for sampling out electrons was suggested by the Ferminet paper. For the initial sampling, a 3D gaussian was taken around the nucleus, which gets improved over the time as steps are taken.
Corresponding pull requests:
https://github.com/deepchem/deepchem/pull/2935
(The sampler was implemented in numpy and is part of the deepchem utils, so that it can be used later. Additionally, an extra option of symmetric and asymmetric moves for taking the samples were given.) -
2. KFAC-optimizer:
Next down in the line was the Kronecker-Factored approximate curvature optimizer or KFAC in short (https://arxiv.org/pdf/1503.05671.pdf).
It is an approximate second-order optimizer which approximates the hessian to make the computation faster as in a normal second-order optimizer, the rate determining step is the hessian calculation. The use of hessians in second-order optimizers brings in more information about the direction of the step which should be taken and hence helps in reducing the number of steps. Thus KFAC makes a tradeoff between the accuracy and time here. The reason to use a second-order optimizer is that the optimizer uses less steps than a first-order optimizer(which usually takes less time per step)
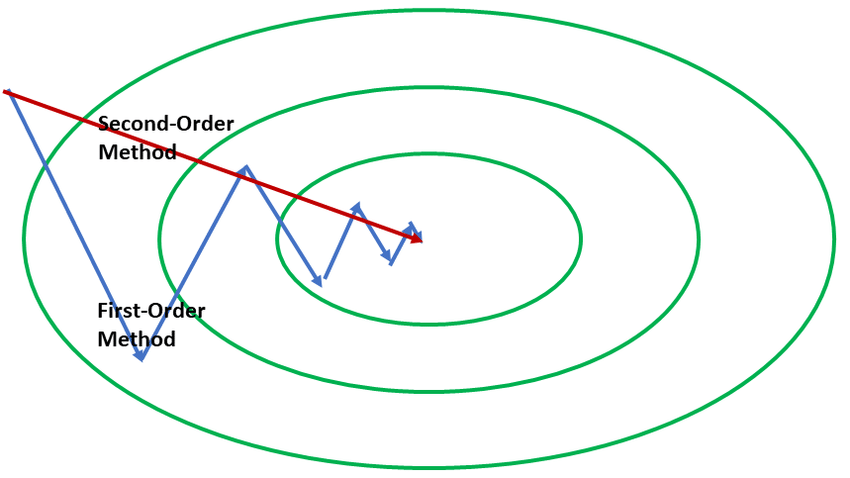
(source: Google images)
(Here the first order optimizer takes a multiple zig-zag path while the second order optimizer takes in a single straight path.)
Special thanks to Chaoqi Wang(https://github.com/alecwangcq), as much of the code was inspired from his pytorch implementation of KFAC.
Corresponding pull requests:
-
3. Ferminet Model
The Ferminet Model requires only the nucleus position from which electrons will be sampled and will be operated on. The model takes in 2 vectors:-- one-electron stream: All possible vectors between the nucleus and the electron position.
- two-electron stream: All possible vectors between any 2 electrons in the molecule system.
These two streams of data aim to incorporate the missing electron-electron repulsion factor and is fed into the DNN.
Also, the electrons are segregated according to their spin(up-spin and down-spin).Corresponding pull requests:
https://github.com/deepchem/deepchem/pull/2997Then comes in the model implementation itself. Ferminet has variable input-sizes according to the molecule chosen (the number of nuclei and electrons), and sometimes a projection matrix might be used in the place of skip-connections whose dimensions will again vary according to the molecule taken.
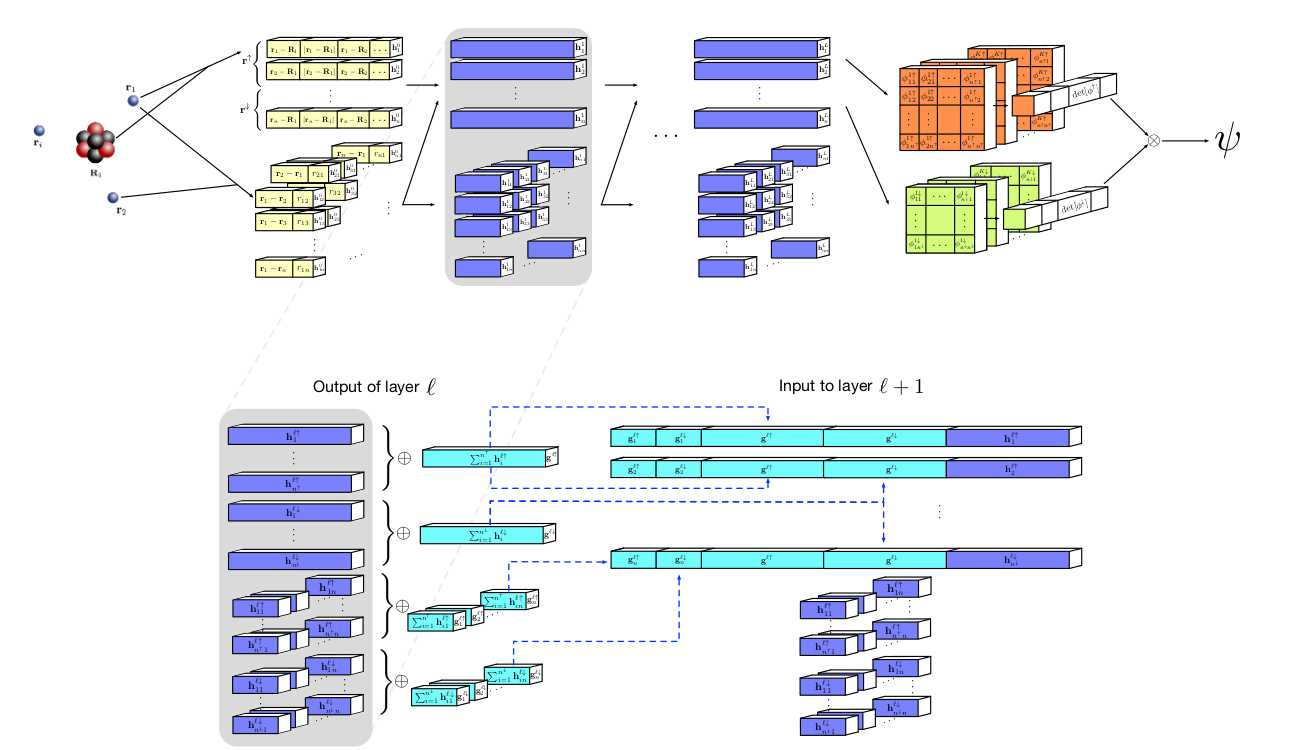
(Source: Ferminet paper)
The model is as illustrated above. The two-electron features are concatenated with one-electron feature in each layer, but the vice-versa is not observed. In the end each orbital will have its own corresponding block of electron-spin tensor, whose determinants are taken and concatenated at the end to get a wavefunction. Moreover, boundary conditions are also imposed in the model, which decreases the probability of finding an electron with increasing distance from the nuclei and 0 at infinity.Ferminet also pretrains to match up to the baseline Hartree-Fock solution ( PySCF was used primarily to get these solutions) using ADAM as the optimizer and half of its sample from the obtained wavefunction and part from the HF solution. Then it is trained normally using KFAC and electrons are sampled from the obtained wavefunction from the model.
For the pretraining, a simple loss statement with expected value of the difference between Hartree-Fock solution and the obtained solution. For the actual training the hamiltonian energy of the system is computed using hessians and jacobians, and the expected value of this value and the gradient with respect to the parameters of the model are taken as the loss. One challenge I encountered while implementing this loss was ‘NaNs’ which were coming as the result from the calculation of hessian. Only after using the anomaly detection tool for NaNs, and scouring through the code, epsilon was missing in the long lines of code while calculating the norm of the one-electron and two-electron vector which seems to have caused the error!!! Some of the tool which I have used for troubleshooting for finding the specific line were “detect_anomaly()” for the specific line number and the “torchviz” package to visualize the autograd graph.
corresponding pull requests:
https://github.com/deepchem/deepchem/pull/3039
https://github.com/deepchem/deepchem/pull/3027
Miscellaneous pull requests:
Future Changes and scope for improvement:
The electron initialization for the sampling is right now done on the basis of the most electronegative atom in a molecule, but this leads to a problem when there are multiple charges and multiple atoms of the same element. To tackle this problem, one can use the partial charges computed from the Hartree-Fock calculation which can also be done using PySCF.
Another scope of improvement can arise from the integrating some of the features of Paulinet(https://arxiv.org/abs/1909.08423) , which incorporates the physical boundary condition of the orbitals, this can further significantly improve the speed of the model with a very little compromise on the accuracy.
Other types of sampling methods like Hamiltonian Monte Carlo can also be tried and tested out.
Also, I am planning to write a Colab tutorial on the usage of the Ferminet model, which I will post in the below thread once complete!
Acknowledgement:
Thanks to my mentors- Tony Davis and Dr. Peter Eastman, for helping throughout my project and supervising it. Thanks to Dr. Bharath Ramsundar for his advice when I got stuck at some points. Special thanks to Dr. David Pfau from Deepmind (One of the authors of Ferminet ) for his clarifications and discussions about the model.
Edit: Updating for Shai since he doesn’t have forum credit to make edits yet
