
This summer I got selected for Google Summer of Code as a contributor in Deepchem which is an Open-Source initiative that aims to democratize the use of deep learning in various fields, such as drug discovery, material science, quantum chemistry, and biology. It provides high-quality tools that enable researchers to use deep learning to address complex problems in these fields.
In this forum post, I’ll provide a detailed summary of the tasks I worked on and the progress I made over the summer.
Project Title : Hamiltonian Neural Network
My project focused on implementing a Hamiltonian Neural Network (HNN), which was part of the Deepchem Model Wishlist.
Some Important links :
Project page: https://summerofcode.withgoogle.com/programs/2025/projects/NBfvsztr
My Github: https://github.com/a-b-h-a-y-s-h-i-n-d-e
My linkedin: https://www.linkedin.com/in/abhay-shinde-4b1a7a23b/
Deepchem Home page: https://deepchem.io/
Deepchem github: https://github.com/deepchem/deepchem
Proposal link: Google docs link
Slides deck: Google Slides link for each week
Preface :
Hamiltonian Neural Networks (HNNs) are a physics-inspired deep learning approach that learns the Hamiltonian function of a system instead of directly modeling its trajectories. The Hamiltonian represents the total energy of a system (kinetic + potential), and by learning it, HNNs can capture the underlying dynamics in a way that is consistent with physical laws like conservation of energy.
Unlike traditional neural networks that may overfit or ignore fundamental structure, HNNs embed prior knowledge of physics into the model. This makes them more interpretable, generalizable, and accurate when simulating complex dynamical systems, making them especially valuable in scientific and engineering domains where preserving physical consistency is crucial.
Contents covered in this forum :
- Expected Deliverables
- Pull Requests
- HNN vs NN
- HNN architecture
- Gradients Calculations
- Usage of HNN model
- Acknowledgment
- References
Pull Requests :
#4465 – Implementing Base HNN layer, test cases and updated docs ( models.rst )
#4475 – Implementing Deepchem Model ( TorchModel ), test cases and updated docs (models.rst )
#4497 – Deepchem Tutorial for HNN
#4502 – correcting equations in tutorial and minor grammer mistakes
#4503 – New test case for HNN model testing on a experiment dataset
HNN vs NN :

Image source: Greydanus – Hamiltonian NNs
Hamiltonian Neural Networks (HNNs) differ from conventional neural networks in that they incorporate the underlying physical structure of a system into the learning process. Unlike standard neural networks, which approximate input-output mappings without constraints, HNNs are designed to preserve key physical invariants , such as energy, by explicitly modeling the system’s Hamiltonian. This structural bias allows HNNs to generalize better for dynamical systems governed by physical laws.
HNN architecture

Image source: Science Direct Article
Hamiltonian Neural Networks (HNNs) take the system’s generalized momenta p and coordinates q as input and feed them into a standard feedforward neural network. The network outputs a single scalar value, the Hamiltonian H(p, q), which represents the total energy of the system. Unlike conventional neural networks that directly predict the next state, the HNN leverages this scalar energy function to ensure that physical invariants, such as energy conservation, are respected.
Once the Hamiltonian is computed, the network uses automatic differentiation to calculate the gradients of H with respect to its inputs. These gradients are then used in Hamilton’s equations to obtain the time derivatives:
- q̇ = ∂H / ∂p
- ṗ = - ∂H / ∂q
This approach allows the HNN to predict the system’s dynamics while maintaining consistency with the underlying physical laws, providing more interpretable and stable long-term predictions compared to standard neural networks.
Gradients Calculations :
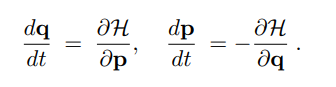
Image source: Research Paper
In Hamiltonian Neural Networks, after computing the scalar Hamiltonian H(p, q), the system’s dynamics are obtained by differentiating H with respect to the inputs. The gradients provide the time derivatives of p and q, ensuring that the predicted evolution respects physical laws such as energy conservation.
from torch.autograd import grad
# Combine momenta and coordinates
z = torch.cat([p, q], dim=-1)
if not z.requires_grad:
z = z.requires_grad_(True)
# Forward pass through the network to get Hamiltonian
H = self.net(z).squeeze(-1)
# Compute gradients w.r.t inputs
grad_H = grad(H.sum(), z, create_graph=True)[0]
# Split gradients into dq/dt and dp/dt
dim = z.shape[-1] // 2
dH_dq = grad_H[..., :dim]
dH_dp = grad_H[..., dim:]
dq_dt = dH_dp
dp_dt = -dH_dq
Usage of HNN model :
Hamiltonian Neural Networks (HNNs) are particularly useful for modeling physical systems where energy conservation plays a key role, such as in classical mechanics, orbital dynamics, and molecular simulations. They are often applied in areas like physics-informed machine learning, robotics, and scientific computing, where capturing the underlying symmetries and conservation laws of a system leads to more accurate and interpretable predictions
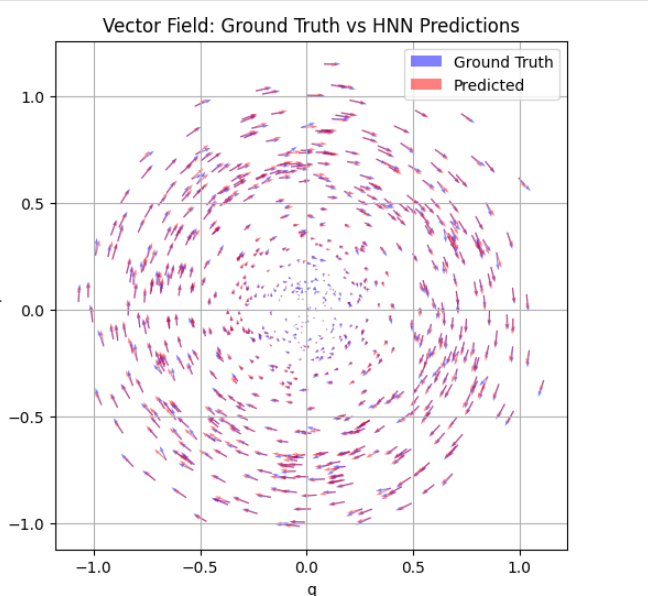
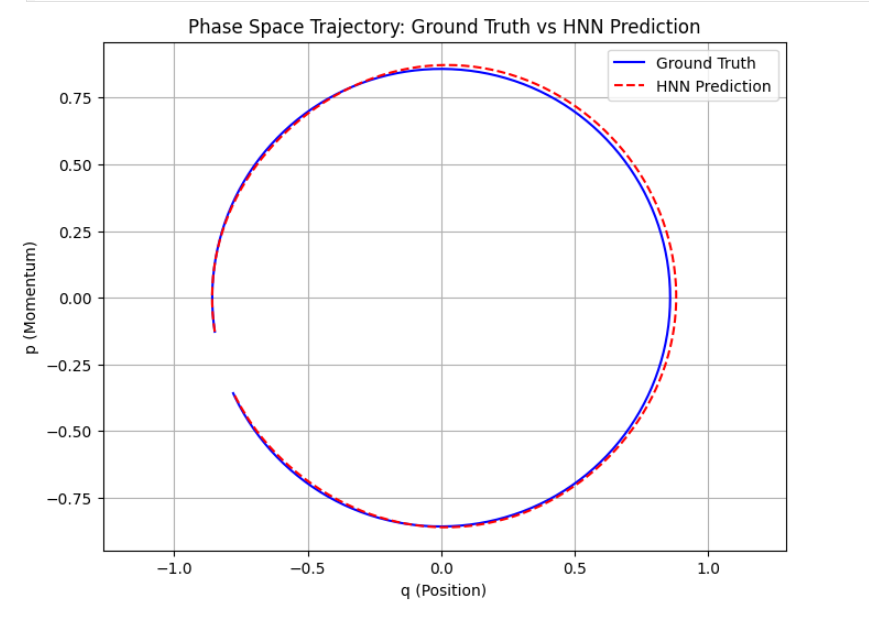
I have created begineer friendly Deepchem tutorial for HNN model along with visualizing the results/predictions, it will be visible on deepchem.io in next release of deepchem ( check the tutorials page ) but you can also check the raw notebook file here - [LINK]
In this tutorial, we simulate a simple physical system governed by Hamiltonian dynamics to demonstrate the capabilities of HNNs. The implementation leverages DeepChem’s existing abstractions, such as TorchModel for model training and evaluation, and NumpyDataset for managing the input data. Using these components, we trained and tested an HNN to learn the dynamics of the system.
Acknowledgment
Forever grateful to my mentor José A. Sigüenza for his guidance and support, and deeply thankful to Bharath Ramsundar for believing in my potential. Also thankful to mentors such as Rakshit Singh, Shreyas, Aaron for helping me throughout my journey.
Being a part of this organization has given me valuable insights into the practical aspects of machine learning and its real-world applications.
References
[1] Greydanus, S., Dzamba, M., & Yosinski, J. (2019). Hamiltonian Neural Networks. arXiv:1906.01563
[2] Steve Brunton video about HNN
[3] Jax implementation : Scibits article
[4] Github Repository from Author
[5] Science direct article on HNN
